Рубин является одним из самых известных кристаллов, использующихся в квантовой электронике. На нем создан малошумящий парамагнитный усилитель, а также первый лазер, работающий в оптическом и ближнем ИК диапазонах на нескольких длинах волн. Активными центрами в рубине являются ионы хрома Cr³⁺. С теоретической точки зрения оказывается очень важным уметь рассчитывать уровни энергии этих ионов, которые отождествляются с энергией электронного облака, для получения частот переходов между этими уровнями.

Движение электронов в атомах и ионах подчиняется законам квантовой механики. Для получения их уровней энергии нужно согласно общим правилам составить оператор Гамильтона и найти его собственные значения, которые и есть энергиями уровней. Однако точный гамильтониан оказывается настолько сложным, что решение с ним данной задачи не представляется возможным. Поэтому пользуются упрощениями, которые приводят к разным намного более простым гамильтонианам для разных групп уровней.

Здесь описывается расчет енергий самой нижней компактной группы, состоящей из четырех уровней, и обозначаемой как ⁴A₂. Именно эти уровни заселены при комнатной температуре. Так как кристалл рубина является парамагнитным веществом, энергии рассчитываются с учетом присутствия постоянного магнитного поля и с учетом анизотропии свойств кристалла.

Состояние ⁴A₂ иона Cr³⁺ описывается следующим упрощенным гамильтонианом, который называется еще эффективным, а также спиновым гамиьтонианом:

Здесь g = 1,985 - фактор Ланде, μ_B - магнетон Бора, D - постоянная кристаллического ращепления, равная -0,3831 см^-1, B - индукция постоянного магнитного поля, S_z, S_x - декартовые компоненты, а S² - квадрат оператора спина . Ось z направлена вдоль оси симметрии кристалла, ось x перпендикулярно к ней.

Если ввести обозначение , а также определить угол θ между осью симметрии кристалла и направлением вектора индукции магнитного поля, то гамильтониан можно переписать в более компактном виде:

Операторы S_z, S_x и S² это матрицы. Для спина S = 3/2 размер матриц равен (2S+1) = 4. Их вид в базисе, в котором матрицы S_z и S² диагональны, следующий:

Гамильтонианы (1) - (2), записанные в матричном виде, имеют размер 4×4. Построение матриц гамильтониана проводится подстановкой матриц (3) - (5) в выражения (1), (2). При этом необходимо выполнить все предписанные арифметические операции. Умножение матриц на скалярные величины ξ, cosθ, sinθ, 1/3 состоит в умножении каждого элемента матрицы на эту величину. Сложение и вычитание матриц производится поэлементно, умножение матриц производится по законам матричной алгебры, которое на бытовом уровне звучит как "строка на столбец". Для примера ниже показано как вычисляется элемент гамильтониана (2).

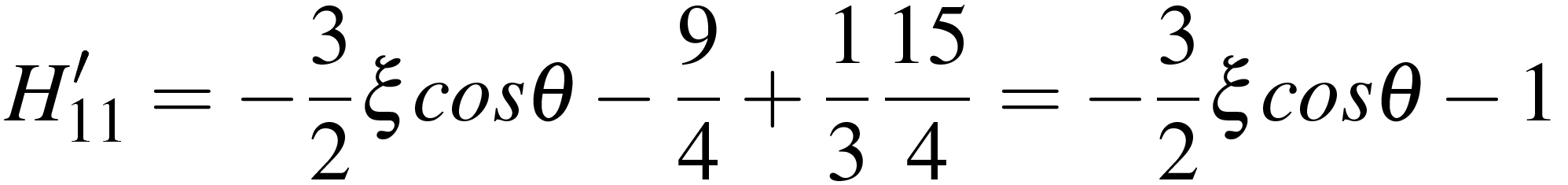
Собственные значения можно найти из условия обращения в 0 детерминанта матрицы, которая получается из матрицы гамильтониана вычитанием из диагональных членов искомого собственного значения ε.

Если ввести сокращенные обозначения c для cosθ и s для sinθ, то матрица для вычисления детерминанта может быть записана в следующей компактной форме:

Раскрытие детерминанта приводит к характеристическому степенному уравнению четвертого порядка, которое имеет четыре корня, - уровня энергии. Аналитически вычислить эти корни можно только для определенных значений угла θ, а именно, 0°, когда sinθ=0 и cosθ=1, и 54.7356°, когда cosθ=1/√3.

В общем же случае для произвольных значений угла θ следует прибегать к численным методам нахождения собственных значений. Для этого была составлена простая программа на Python, которая рассчитывала собственные значения спинового гамильтониана (2) для заданных углов θ и строила графики зависимостей уровней энергии от величины внешнего магнитного поля. Ниже приведены четыре рисунка для θ=0°, 30°, 60° и 90°.

Программа на Python использовала модули numpy и scipy для построения матрицы гамильтониана и нахождения собственных значений и модуль matplotlib.pyplot для отрисовки зависимостей, приведенных на вышерасположенных рисунках.

Программа

	
# Energies of CR3+ in ruby.

from numpy import pi, cos, sin, sqrt, linspace, zeros, array, append
from numpy.linalg import eigvalsh
from scipy.constants import physical_constants as phc
from matplotlib.pyplot import figure, title, ylabel, xlabel, \
xlim, xticks, yticks, plot, grid, tight_layout, savefig, show

angle = 90. # angle theta.
Bmax = 10000.

def SxMatrix(Sx):
    ''' Sx matrix '''
    for i in range(1,4):
        m = i - 2.5
        me = sqrt(3.75 - m * (m+1))/2.
        Sx[i-1][i] = Sx[i][i-1] = me

def SzMatrix(Sz):
    ''' Sy matrix '''
    for i in range(0,4):
        Sz[i][i] = i - 1.5

def Hdmatrix(Hd):
    ''' Const matrix which is equal Sz**2 - s(s+1)/3 '''
    for i in range(0,4):
        Hd[i][i] = (i - 1.5)**2 - 1.25
              
def HamltnD(D, gpar, gprp, b, thetazx, Sx, Sz, Hd):
    ''' Hamiltonian for a given B '''
    bz = b * cos(thetazx * pi / 180.)
    bx = b * sin(thetazx * pi / 180.)
    return gpar*bz*Sz + gprp*bx*Sx-D*Hd

Bfield = linspace(0., Bmax, 50)

# ----- constants ----------
# mub = 4.6693e-5  # Bohr magneton cm-1/gauss
# mub = 1.39962  # Bohr magneton MHz/gauss
# Bohr magneton cm-1/gauss
mub = phc['Bohr magneton in inverse meters per tesla'][0]/10**6 
# Bohr magneton MHz/gauss
mub = phc['Bohr magneton in Hz/T'][0]/10**10 

D = -5743. # D/2 (MHz)
gpar = 1.9840 # g parallel (dimensionless)
gprp = 1.9867 # g perpendicular (dimensionless)
gpar *= mub
gprp *= mub

Sz = zeros((4,4))
Sx = zeros((4,4))
Hd = zeros((4,4))
SxMatrix(Sx)
SzMatrix(Sz)
Hdmatrix(Hd)

# Calculated energies are in MHz
entot = array([])
for hf in Bfield:
    H = HamltnD(D, gpar, gprp, hf, angle, Sx, Sz, Hd)
    e = eigvalsh(H)
    entot = append(entot,e)

fig = figure(figsize = (12,8))
title("Уровни энергии для угла " + str(angle) +"$^o$\n", fontsize = 20)
ylabel("Энергия (ГГц)", fontsize = 20)
xlabel("\nИндукция магнитного поля (Гаусс) * $10^{-3}$", fontsize = 20)
xlim(0,Bmax/1000)
xticks(fontsize = 18)
yticks(fontsize = 18)

for k in range(4):
    plot(Bfield/1000, entot[k::4]/1000, lw=2, color = 'blue')

grid()
tight_layout()
savefig(str(angle) + '.jpeg')
show()
	

Данная страница является частью раздела "Электронный парамагнитный резонанс".